Edward Lorenz: The Mathematics of Unpredictable Weather and Strange Attractors

Because Our Climate Measurements Are Imprecise, the IPCC Mathematical Models Predicting Global Warming Are Mathematical Nonsense

Excerpt from my book The Truth About Energy, Global Warming, and Climate Change: Exposing Climate Lies in an Age of Disinformation

When applied to the atmosphere, the power of Lorenz’s discovery is that any variations in measurement will produce enormous differences in outcomes. Mathematically this is impossible to avoid. To understand this, please consider that equally divisible numbers can be divided by other integers with no remainders. For instance, the number “4” is equally divisible by the number “2,” while the number “7” cannot be equally divided by “2.” An irrational number is a number that can be expressed as a decimal but not as a fraction. Irrational numbers are not the ratio of two integers.

For instance, π (Pi), the ratio of a circle’s circumference to its diameter, is the irrational number 3.141592, etc. An irrational number has an infinite series of numbers after the decimal because an irrational number is never fully divisible. Temperature variables as simple as “degrees Celsius,” to be precise, are of necessity measured in irrational numbers. Irrational numbers are characterized by infinite numbers lying to the decimal’s right with increasingly more accurate measurements. Understanding the concept of infinity is mathematically tricky. No matter how many decimal places we calculate for an irrational number, there yet remain an infinitely greater number of additional decimal places that we have yet to figure. That irrational numbers are followed by an infinitely calculable number of decimal places means no human being will ever mathematically calculate the last remaining decimal place.

In contrast, nature does not need to calculate decimal places. Irrational numbers and their operation are intrinsic to the fabric of the mathematical logic by which nature operates just fine, without any assistance from human beings. The point is that the unavoidable use of irrational numbers in climate model measurements means Lorenz’s problem with slight differences in initial calculations never goes away. This problem alone prevents any computer from accurately predicting weather or climate, no matter how powerful the computer might be.

In analyzing weather and climate, we must remember that nature does not worry about computing decimal points. But climate outcomes will be different because a computer model cannot compute infinite decimal places. Even computers set to calculate an enormous number of decimal places have limits. After calculating a vast number of decimal places, an endless number of decimal places still remains to be calculated. Human beings and computers cannot calculate infinite sets. But, again, nature operates without having to conduct human calculations and without needing computers. One of the leading reference books on chaos theory and fractal mathematics points out the problem as follows:

In other words, even if the weather models in use were absolutely correct—that is, as models for the physical development of the weather—one cannot predict them for a long time period. The effect is nowadays called sensitive dependence on initial conditions. It is one of the central ingredients of what is called deterministic chaos.¹

When we add positive and negative feedback effects into the climate model, the outcome is as follows:

Eventually the iterations of our feedback process become as trustworthy as if we had obtained them with a random number generator, or rolling dice, or flipping coins. In fact, the Polish mathematician Stan Ulam discovered that remarkable property when he constructed numerical random number generators for the first electronic computer ENIAC in the late forties in connection with large scale computations for the Manhattan Project.²

Yet another sort of measurement problem makes weather prediction impossible. Again, this problem derives from fractal mathematics. The problem is known as the “coastline paradox.” As author James Gleick explained, “any coastline is—in a sense—infinitely long.” ³ The length of the coastline depends on how the coastline is measured. Mathematician Benoit Mandelbrot elaborated the paradox this way in his 1973 book The Fractal Geometry of Nature:

When a bay or peninsula noticed on a map scaled to 1/100,000 is reexamined on a map at 1/10,000, subbays and subpeninsulas become visible. On a 1/1,000 scale, sub-subbays and sub-subpenninsulas appear, and so forth. Each adds to the measured length.⁴

In a study of fractals applied to legal questions and lawsuits, David Post, a professor at the Beasley School of Law, Temple University, and his coauthor Michael Eisen at the Lawrence Berkeley National Laboratory, and the Department of Molecular and Cellular Biology, University of California, Berkeley, made an interesting comment about the fractal methodology for measuring coastlines. Post and Eisen noted that “true fractal objects” are “those for which (by definition) estimated length L() never converge.” In Euclidian geometry, for instance, the length of the circumference of a circle is estimated by multiplying the diameter of the circle by .

As we have just seen, the answer will not be a perfectly precise number because , 3.14, is an irrational number. But the point Post and Eisen wanted to make about fractal math is that in Euclidian geometry, the measurement of the circumference converges on the value of the circle’s diameter multiplied by . In Euclidian geometry, our measurement value will converge on the measurement estimated by the formula C = d, where C is “circumference” and “d” is diameter, as the measuring rulers get smaller and smaller. Post and Eisen stated the point as follows: “Our estimating procedure will—must—converge on this value as our rulers get smaller and smaller; we may need an infinite number of infinitesimally small rulers to get it exactly correct, but Euclidian geometry is premised on the notion we can do just that.” But true fractal objects, they point out, by contrast are those for which (by definition) estimated length L() never converges. “Fractals appear to get longer and longer as the measuring stick gets smaller and smaller, and the estimated length of a true fractal diverges to infinity as  approaches zero,” they explained.⁵

Stated another way, a principle of fractal math is that measurement totals change as the dimension of the measurement is reduced. A map of the Dover coast on the English Channel gives one measure for the coastline length that differs from the measurements made walking along the Dover coast. Gleick explained the point as follows: “But Mandelbrot found that as the scale of measurement becomes smaller, the measured length of a coastline rises without limit, bays and peninsulas revealing ever-smaller subbays and subpeninsulas—at least down to atomic scales, where the process does finally come to an end. Perhaps.” ⁶

We are back to infinity again, and the same problem applies. We can never get a precise measurement because of the limitations in our measuring technology, whether the measuring technology is an ordinary ruler or an electron microscope. Thus, all our weather measurements are limited by the measurement instruments we utilize. Temperature measurements in Celsius or Fahrenheit are crude measurements compared to nature. Again, nature needs no ruler or any other measurement instrument to operate the weather. Our climate models are doomed to suffer from slight differences in initial states because the values we enter for critical variables like temperature, wind speed, etc. are inherently imprecise because of the coastline paradox in fractal mathematics.

So, as Lorenz demonstrated, weather prediction (and hence prediction of the climate) is impossible for several reasons. First, the environmental variables that need to be in a climate model approach being an infinite set. Second, the interaction between the independent and dependent variables in the computer model is inherently nonlinear. Third, the measurement of essential variables will involve irrational numbers, which inherently involve an infinite number of decimal place calculations. Fourth, the coastal paradox problem in fractal math means the measurement of weather variables generates results that approach infinity as our measuring instruments get increasingly fine, approaching zero, i.e., as we operate at increasingly more detailed levels of observation, down to the subatomic level. Nature suffers none of these problems. Weather and climate do not need human measurements or computer calculations to operate on Earth.

Lorenz understood from these calculations that the weather system lacks predictability that no computer can overcome, regardless of how powerful. What Lorenz demonstrated is that chaos is an inherent feature of the weather system. “Chaos wipes out every computer,” the reference book on chaos and fractals insists. “The fact is that no matter how small a deviation in the starting values we choose, the errors will accumulate so rapidly that after relatively few steps the computer prediction is worthless.”⁷

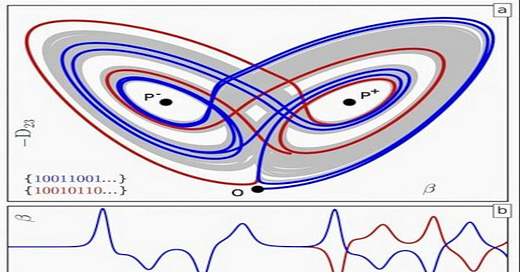
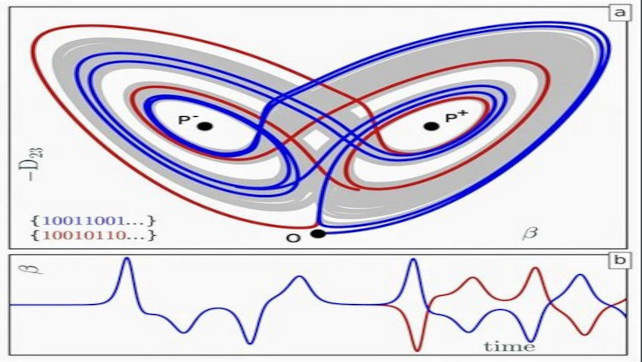
Yet, when Lorenz modeled the equations in his 1963 paper, he found the flow patterns of his twelve equations were not entirely random. Instead, seen in three-dimensional space, his observations graphed around two separate but related points that graphically look like a butterfly’s wings. The two points around which the observations clustered are known as “Lorenz Strange Attractors.” The point is that the calculations remained unpredictable, even though the calculations tended to cluster around two distinct points on the graph.

Some comments made by Steven Koonin, the former undersecretary for science in the Energy Department under the Obama administration, helps make the point. “Climate is not weather,” Koonin stressed in his 2021 book Unsettled. “Rather, it’s the average of weather over decades, and that’s what climate models try to describe.”⁸ What Lorenz proved with the climate model he ran in his MIT office, on an early Royal McBee LGP-30 digital computer, was not that weather is random but that it is not predictable. The point is that even extreme weather in the form of severe floods, hurricanes, tornadoes, etc., is a natural feedback mechanism Earth uses to distribute heat around the planet. But usual weather features, including sunny days, rain, snow, etc., and extreme weather events like floods, hurricanes, and tornadoes are recurring weather patterns, even if not entirely predictable. In chaos theory, weather events are the strange attractors that constitute what we call climate.

A seven-day weather forecast can accurately predict the weather about 80 percent of the time, and a five-day forecast can accurately project the weather approximately 90 percent of the time.⁹ But the farther out the prediction, the less reliable the weather forecast will be. A ten-day forecast is at the “practical predictability limit,”¹⁰ right only about half the time. James Gleick understood this point when writing his 1987 book Chaos. Gleick imagined the earth covered with sensors spaced one foot apart, rising at one-foot intervals to the top of the atmosphere. He further assumed every sensor gave perfectly accurate estimates of every variable a meteorologist would want, including temperature, pressure, and humidity. “Precisely at noon an infinitely powerful computer takes all the data and calculates what will happen at each point at 12:01, then 12:02, then 12:03…,” Gleick imagined. “The computer will still be unable to predict whether Princeton, New Jersey, will have sun or rain on a day one month away,” Gleick explained.¹¹

Lorenz’s scientific papers make clear that the inability to predict the weather accurately will not go away when our computers become quantum computers. The limits Lorenz identified do not derive from relativity theory. As weather observational technology advances, we will have an increased ability to predict the weather for the next few days. But even with highly advanced weather observational technology and quantum computers, the complexity of climate models, as demonstrated by Lorenz, means weather forecasting will never be accurate except for very near-future periods. As a rule of thumb, the best prediction for tomorrow’s weather still is to know what the weather is doing today. But the fact that seasonal weather will change Earth’s temperature necessitates the conclusion that the methodology of predicting tomorrow’s weather from today’s weather only works in the short term.

Those few IPCC climate experts who retain some shred of intellectual honesty and academic integrity have been willing to acknowledge the folly of IPCC climate models predicting CO₂ disasters from the burning of hydrocarbon fuels. In June 2007, James Renwick, a professor in the School of Geography, Environment, and Earth Sciences at the Victoria University of Wellington and a top IPCC scientist, stated on New Zealand Radio that “[t]he weather is not predictable beyond a week or two.” He admitted the IPCC climate models were not reliable. “Climate prediction is hard, half of the variability in the climate system is not predictable, so we don’t expect to do terrifically well.”¹²

Another high-profile IPCC lead author, Dr. Kevin Trenberth, a distinguished scholar at the National Center of Atmospheric Research (NCAR) in Boulder, Colorado, admitted IPCC climate models were merely “story lines.” In a 2007 “Predictions of Climate” blog post appearing in the science journal Nature, Trenberth admitted the following: “None of the models used by IPCC are initialized to the observed state and none of the climate states in the models correspond even remotely to the current observed climate. In particular, the state of the oceans, sea ice, and soil moisture has no relationship to the observed state at any recent time in any of the IPCC models.” In that blog Trenberth was particularly blunt. “In fact there are no predictions by IPCC at all. And there never have been,” he wrote. “The IPCC instead proffers ‘what if’ projections of future climate that correspond to certain emissions scenarios.”¹³

IPCC reviewer and climate researcher, Vincent Gray, now deceased—the founder of the New Zealand Climate Science Coalition, a reviewer of every single draft of the IPCC reports going back to 1990 through 2014, author of more than one hundred scientific publications, and author of The Greenhouse Delusion: A Critique of “Climate Change 2001”¹⁴—declared in 2007 that “[t]he claims of the IPCC are dangerous unscientific nonsense.”¹⁵ Gray went on to claim that no IPCC climate model “has ever been properly tested, which is what ‘validation’ means, and their ‘projections’ are nothing more than the opinions of ‘experts’ with a conflict of interest, because they are paid to produce the models.” Gray went on to say, “There is no actual scientific evidence for all these ‘projections’ and ‘estimates.’ It should be obvious that they are ridiculous.”¹⁶

Yet, the IPCC insists on understanding Earth’s weather and climate in linear terms, targeting CO₂ as the sole variable responsible for global warming. That the IPCC can confidently say that continued burning of hydrocarbon fuels will mean Earth’s temperature will rise more than 1.5°C above preindustrial levels by 2030 or 2050 is nonsense. In a nonlinear climate system, any number of nonpredictable events may occur. The sun might flare or otherwise increase activity. Equally possible, the sun might already be entering a new minimum period. In time-series analysis, the variations of temperature recorded over a few years are too short a period to establish a new Earth temperature phenomenon statistically. In geological time, time-series climate analysis requires hundreds of thousands or even millions of years of accurate data to be meaningful.

---

The gases and dust a volcano throws into the atmosphere can have a global cooling effect regardless of how much CO₂ there is in the atmosphere. Thus, a cataclysmic event such as a massive volcanic eruption or a series of cataclysmic events such as a series of volcanoes erupting might dramatically cool Earth even if CO₂ concentrations were at prehistoric levels. Between June 12 and June 15, 1991, the sulfur dioxide emitted by the eruption of Mt. Pinatubo in the Philippines lofted an ash plume more than twenty kilometers into the atmosphere, throwing fifteen million tons of SO₂ into the stratosphere. The SO₂ reacted with water vapor to create upper atmosphere aerosols that reflected incoming sunlight. The Pinatubo eruption increased aerosol optical depth in the stratosphere by a factor of ten to one hundred times normal levels as measured before the eruption. Aerosol optical depth is a measure of how much light airborne particles prevent from passing into the atmosphere. As a result, the eruption of Mt. Pinatubo caused Earth’s mean surface temperature to decrease by about 0.6°C (1.0°F) over the next fifteen months.¹⁷

An extraterrestrial event may occur, such as another Chicxulub-size asteroid hitting Earth. Unusually high supernova activity could bombard Earth with cosmic rays. Recent scientific studies of supernovas and cosmic rays have stressed that historical and archeological evidence of global warming and cooling that occurred long before the Industrial Revolution “require natural explanations.” Danish physicist Henrik Svensmark, whose work on supernovas we reviewed extensively in chapter 5, published a paper in 2015 in which he concluded that since “supernova variation reflects variation in star formation and the morphology of our Galaxy’s spiral arms, one ends up with the surprising result that the conditions for life on Earth are a reflection of the shape of the Milky Way.” Svensmark concluded that in geological time, supernova activity affected bio-productivity occurring in the cold intervals associated with the star-forming regions, regardless of how much CO₂ was in the atmosphere. “Biodiversity and bio productivity [as measured by studies of δ¹³C, i.e., the carbon-13 isotope] all appear so highly sensitive to supernova in our Galactic neighborhood that the biosphere seems to contain a reflection of the sky.”¹⁸ Or Earth’s climate thermometer might simply continue to adjust the CO₂ level on Earth such that the interglacial period we are experiencing could extend another 10,000 or more years.

But Gleick understood the idea that weather and, consequently, the climate are inherently unpredictable would go against the grain of experienced meteorologists. One of Lorenz’s oldest friends was Robert White, a fellow meteorologist at MIT who later became head of the National Oceanic and Atmosphere Administration. Lorenz told him about the Butterfly Effect. “White gave von Neumann’s answer. ‘Prediction, nothing,’ he said. ‘This is weather control.’” Gleick explained White’s thought was that small modifications, well within human capability, could cause desired, large-scale changes. For White, small, unpredictable weather outcomes did not change the reality that weather follows a deterministic logic where climate processes can be modeled precisely such that human intervention could yet have outcomes that were predictable according to the climate laws that were fully understood.

Lorenz not only disagreed, he felt White’s conceptual weather paradigm was outmoded. Lorenz explained to White that we human beings can change the weather, but you would never be able to predict the outcome. “Yes, you could change the weather,” Lorenz told White. “You could make it do something different from what it would otherwise have done. But if you did, then you would never know what it would otherwise have done,” Lorenz explained. “It would be like giving an extra shuffle to an already well-shuffled pack of cards. You know it will change your luck, but you don’t know whether for better or worse.”¹⁹

The Butterfly Effect, the logic of nonlinear equations, and the impact of fractal math were the reasons why mathematically based computer-driven climate models are doomed to failure, why long-term weather predictions are rarely correct, and why human climate interventions suffer from the laws of unintended consequences. “For small pieces of weather—and to a global forecaster, small can mean thunderstorms and blizzards—any prediction deteriorates rapidly,” Gleick noted, explaining the Butterfly Effect. “Errors and uncertainties multiply, cascading upward through a chain of turbulent features, from dust devils and squalls up to continent-size eddies that only satellites can see.”²⁰

---

1 Heinz-Otto Peitgen, Hartmut Jürgens, and Dietmar Saupe, Chaos and Fractals: New Frontiers of Science (New York and Berlin: Springer, 1992), p. 48.

2 Ibid.

3 James Gleick, Chaos: Making a New Science, pp. 95-96.

4 Benoit B. Mandelbrot, The Fractal Nature of Nature (New York: W.H. Freeman and Company, 1977, updated and augmented, 1983), p. 26.

5 Ibid.

6 James Gleick, Chaos: Making a New Science, p. 96.

7 Heinz-Otto Peitgen, Hartmut Jürgens, and Dietmar Saupe, Chaos and Fractals: New Frontiers of Science, p. 49.

8 Steven E. Koonin, Unsettled: What Climate Science Tells Us and What It Doesn’t and Why It Matters.

9 “How Reliable Are Weather Forecasts?” SciJinks.com, no date, https://scijinks.gov/forecast-reliability/.

10 Fuqing Zhang, Y. Qiang Sun, et al., “What Is the Predictability Limit of Midlatitude Weather?” Journal of the Atmospheric Sciences, Volume 76, Issue 4 (April 1, 2019), pp. 1077-1091, https://journals.ametsoc.org/view/journals/atsc/76/4/jas-d-18-0269.1.xml.

11 James Gleick, Chaos: Making a New Science, pp. 20-21, at p. 21.

12 Quoted in William F. Jasper, “Computer Models vs. Climate Reality,” New American, Volume 31, Number 8 (April 20, 2015), https://thenewamerican.com/computer-models-vs-climate-reality/.

13 Kevin E. Trenberth, “Predictions of climate,” Blogs.Nature.com, posted on June 4, 2007, http://blogs.nature.com/climatefeedback/2007/06/predictions_of_climate.html.

14 Vincent Gray, The Greenhouse Delusion: A Critique of “Climate Change 2001” (Brentwood, Essex, U.K.: Multi-Science Publishing Co., Ltd., 2004).

15 “IPCC Report slammed as ‘dangerous nonsense,’” New Zealand Climate Science Coalition, Scoop.co.nz, press release, April 10, 2007, https://www.scoop.co.nz/stories/SC0704/S00023.htm.

16 Quoted in the following: U.S. Senate Environment and Public Works Committee, Minority Staff Report, Senator James Inhofe, “More Than 650 International Scientists Dissent Over Man-Made Global Warming Claims. Scientists Continue to Debunk ‘Consensus’ in 2008,” December 11, 2008, p. 129, https://www.epw.senate.gov/public/_cache/files/8/3/83947f5d-d84a-4a84-ad5d-6e2d71db52d9/01AFD79733D77F24A71FEF9DAFCCB056.senateminorityreport2.pdf. All quotations in this paragraph are drawn from the following source: Marc Morano, “UN IPCC Scientist: ‘No convincing scientific arguments to support claim that increases in greenhouse gases are harmful to the climate,’” ClimateDepot.com, May 5, 2009, https://www.climatedepot.com/2009/05/05/un-ipcc-scientist-no-convincing-scientific-arguments-to-support-claim-that-increases-in-greenhouse-gases-are-harmful-to-the-climate/.

17 “Global Effects of Mount Pinatubo,” NASA Earth Observatory, no date, https://earthobservatory.nasa.gov/images/1510/global-effects-of-mount-pinatubo. See also: Cindy Evans, “Astronauts photograph Mt. Pinatubo,” NASA Earth Observatory, June 14, 2001, https://earthobservatory.nasa.gov/features/AstronautPinatubo. See also: “Monitoring the Eyjafjallajökull Eruption,” Climate.gov, NOAA, April 22, 2010, https://www.climate.gov/news-features/featured-images/monitoring-eyjafjallaj%C3%B6kull-eruption.

18 Henrik Svensmark, “Cosmic Rays, Clouds and Climate,” Euro Physic News, 2015, pp. 26-29, https://www.europhysicsnews.org/articles/epn/pdf/2015/02/epn2015462p26.pdf.

19 Reported by Glick in Chaos: Making a New Science, p. 21.

20 Ibid., p. 20.